trokut
Ako su u ravnini nacrtane tri razlličite točke A, B, C koje ne pripadaju istom pravcu one određuju geometrijski lik koji nazivamo trokut. Trokut ABC je dio ravnine omeđen dužinama AB, BC, i CA, uključujući i sve točke tih dužina. Točke ABC su vrhovi, a dužine AB, BC i CA su stranice trokuta. Svaki trokut ima i tri unutarnja kuta.
Trokuti se razlikuju:
- s obzirom na vrste unutarnjih kuteva, a dijele na pravokutane, tupokutane, šiljastokutane trokute
- s obzirom na duljine stranica, a dijele se na raznostraničane, jednakostraničane i jednakokračane trokute.
RAZNOSTRANIČAN TROKUT

ima sve tri stranice različitih duljina.
Opseg trokuta

Površina trokuta





PRAVOKUTAN TROKUT

Stranice pravokutnog trokuta koje zatvaraju pravi kut nazivaju se katete. Stranica koja je nasuprot pravom kutu naziva se hipotenuza.
Posebna svojstva: središte opisane kružnice je u polovištu hipotenuze, ortocentar se nalazi u vrhu kod pravog kuta.

Opseg trokuta

Površina trokuta

JEDNAKOSTRANIČAN TROKUT

je trokut kojemu su sve tri stranice jednake duljine.
Posebna svojstva: središte opisane kružnice, središte upisane kružnice, težište i ortocentar se podudaraju.
Opseg trokuta

Visina

Površina

JEDNAKOKRAČAN TROKUT

je trokut kojemu su dvije stranice jednake duljine.
Posebna svojstva: visina u jednakokračnom trokutu dijeli trokut na dva pravokutna trokuta, središte opisane kružnice, središte upisane kružnice, težište i ortocentar se nalaze na pravcu koji je okomit na osnovicu.
Opseg

Površina

pravokutnik
Pravokutnik je četverokut i geometrijski lik, vrsta paralelograma s četiri prava kuta. Dvije nasuprotne stranice su uvijek jednake duljine, kao i dijagonale.
Duljina dužih stranica se definira kao duljina cijelog pravokutnika, a duljina kraćih kao širina pravokutnika.
Dijagonala


Opseg

Površina

Kvadrat
Poseban oblik pravokutnika kojemu su sve stranice jednake duljine zove se kvadrat.
Sve 4 stranice su mu jednake duljine, nasuprotne stranice su mu paralelne, a dijagonale su mu jednake te se prepolavljaju i sijeku pod pravim kutem.
Dijagonala


Opseg

Površina

krug
definicija kružnice

Skup svih točaka ravnine koje su od zadane točke S udaljene za zadani pozitivni broj r naziva se kružnica. Točka S jest središte te kružnice, a broj r njezin radijus.
definicija kruga
Dio ravnine omeđen kružnicom naziva se krug. Krug je skup svih točaka u ravnini čija je udaljenost od određene točke, koju zovemo središte kruga S, manja ili jednaka određenom broju, koji zovemo polumjer kruga ili radijus r. Promjer kruga jest dužina kojoj pripada središte kruga i čije krajnje točke pripadaju kružnici.
Opseg kruga
Za duljinu polumjera kružnice upotrebljavamo slovo r, a budući da je duljina svake kružnice ujedno i opseg kruga što ga ta kružnica obrubljuje, duljinu kružnice kao opseg kruga označavat ćemo slovom O.

Površina kruga
Površina kruga je ovisna o duljini polumjera kruga r.

Dijelovi kruga
Kružni luk

Dio kružnice omeđen dvjema njezinim točkama naziva se kružni luk. Na slici je prikazana formula za računanje duljine kružnog luka. Duljina kružnog luka neke kružnice je proporcionalan s mjerom središnjeg kuta nad tim kružnim lukom.

Kružni isječak

Dio kruga omeđen dvama polumjerima i kružnim lukom naziva se kružni isječak. Sastoji se od središnjeg kuta i kružnog luka l.
Opseg kružnog isječka je

a površina
Kružni odsječak

Kružni odsječak je dio kruga što ga odsjeca tetiva kružnice.
polukrug

Dio kruga omeđen promjerom i polukružnicom naziva se polukrug.
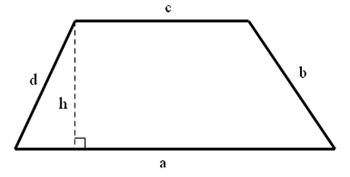
trapez
Trapez je četverokut kome su dvije suprotne stranice paralelne. Nazivamo ih osnovicama, a druge dvije su bočne stranice. Dužina koja spaja sredine bočnih stranica naziva se srednja linija trapeza.
Opseg


Površina

Površina trokuta

Površina pravokutnika

Površina kruga

Površina trapeza