Skalarni i vektorski produkt dvaju vektora iz prostora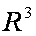

 

Skalarni produkt
 
Neka su i vektori prostora. Bez smanjenja općenitosti, pretpostavimo da oni imaju zajednički početak (postoji jedinstvena točka iz koje polaze ta dva vektora).

DEFINICIJA  

Skalarni produkt vektora i je skalar koji označavamo s i definiramo ovako:
  • ako je jedan od vektora , jednak nulvektoru onda je =0,
  • ako su , različiti od nula, onda je
    ,
    gdje je kut između vektora i takav da je

Funkcija sa zove se SKALARNI PRODUKT. Ta funkcija ima sljedeća svojstva:
(S1) (pozitivna definitnost)
(S2) (pozitivna definitnost)
(S3) (simetričnost)
(S4) (homogenost u prvom argumentu)
(S5) (aditivnost u prvom argumentu)

Račun
 

Vektorski produkt
 
DEFINICIJA  

Vektorski produkt vektora i je vektor takav da je .
Uz to, ako je onda je vektor
Vektorski produkt ima sljedeća svojstva:
(V1) ako i samo ako je = 0 ili =0 ili su vektori i kolinearni
(V2) Vrijedi

(V3) (antikomutativnost)
(V4) (distributivnost)
(V5) norma umnoška jednaka je površini paralelograma što ga razapinju vektori i
Račun