Nelinearni dinamički sustavi

Darko Žubrinić
Zavod za primijenjenu matematiku, FER, Zagreb, 2020.

U Vašem pregledniku treba biti omogućen JavaScript (preporučam da rabite Chrome). Ako nije omogućen, potražite upute putem Googlea, s upitom "enable javascript". U pripremi članka korišten je MathJax (mrežna inačica LaTeX-a) i Processing. Prikaz je u još razvoju.

Ovo je nastavak sljedećih dvaju prikaza:

Matrične transformacije ravnine vizualizirane

Eksponecijalna funkcija matrice i linearni dinamički sustavi


Nelinearni sustavi sa spiralnim trajektorijama

U linearnim sustavima se pojavljuju samo eksponencijalne spirale. Zanimljivo je da se već kod vrlo jednostavnih nelinearnih sustava mogu pojavljivati spirale koje su sasvim drugačije od eksponencijalne spirale. U sljedećem nelinearnom sustavu, \begin{aligned} x_1'(t)&=- x_2(t)-x_1(t)\,[x_1(t)^2+x_2(t)^2]\\ x_2'(t)&=\phantom{-}x_1(t) -x_1(t)\,[x_1(t)^2+x_2(t)^2], \end{aligned} u kojem na desnim stranama imamo polinome trećeg stupnja u dvije varijable \(x_1\) i \(x_2\) (primijetite da linearni dijelovi odgovaraju točno harmonijskom oscilatoru s kružnim trajektorijama u odgovarajućem faznom portretu), nakon kraćeg računa se u polarnom sustavu \((r,\varphi)\) (koristeći \(x_1=r\cos\varphi\) i \(x_2=r\sin\varphi\)), dobiva ovakvo rješenje: $$ r(t)=(2 t+C_1)^{-1/2}, \quad \varphi(t)=t+C_2,\tag1 $$ gdje su \(C_1\) i \(C_2\) konstante.

Doista, množeći prvu jednadžbu sustava s \(x_1\), a drugu s \(x_2\), zbrajanjem dobivamo \(x_1x_1'+x_2x_2'=-(x_1^2+x_2^2)^2\), tj. \(\frac12(r^2)'=r^4\) (naime, \(r^2=x_1^2+x_2^2\)), tj. \(r'=-r^3\) (uz pretpostavku da je \(r\ne0\)). Integriranjem jednakosti \(-r^{-3}dr=dt\) odmah dobivamo \(r(t)=(2 t+C_1)^{-1/2}\).

Iz \(\varphi=\arctan\frac{x_2}{x_1}\) slijedi deriviranjem kompozicije funkcija da je \(\varphi'=\frac{(x_2/x_1)'}{1+(x_2/x_1)^2}=\frac{x_2'x_1-x_2x_1'}{x_1^2+x_2^2}=\frac{x_1^2+x_2^2}{x_1^2+x_2^2}=1\), odakle zaključujemo da je \(\varphi(t)=t+C_2\).

Eliminacijom vremenskog parametra \(t\), iz (1) dobivamo krivulju (gdje priču malo pojednostavnjujemo, odbacivanjem konstanata): $$ r=\varphi^{-1/2}, $$ za kutove \(\varphi\ge\varphi_0\), gdje je \(\varphi_0\) neki zadani pozitivna kut. Ovo je također spiralna trajektorija, ali ona nije eksponencijalnog tipa. Naime, vrijednost \(r=\varphi^{-1/2}\) puno sporije konvergira prema nuli kada \(\varphi\to+\infty\) (tj. kada \(t\to+\infty\)). Već za relativno male vrijednosti kuta \(\varphi\) (tj. nakon svega par okreta duž spirale), vrijednost od \(r\) postaje skoro konstantna, tj. trajektorija postaje skoro kružna! Pogledajte na sljedećem platnu. Ishodište je stacionarna točka, a u ovom slučaju kažemo da je ona slabi fokus.

Ovdje je prikazana spirala \(r=\varphi^{-1/2}\), zadana u polarnom sustavu (dobivena iz nelinearnog sustava opisanog gore). Pritisnite mišem odabranu početnu točku s radius-vektorom \(\mathbf x_0\) i držite ju pritisnutom, da biste vidjeli gibanje točke, kao i pripadajuću trajektoriju (putanju). Ova spirala \(r=\varphi^{-1/2}\), kao funkcija kuta \(\varphi\), konvergira prema ishodištu vrlo sporo kad \(\varphi\to\infty\), a duljina spirale je beskonačna. Ishodište je slabi fokus.

Pogledajmo kako za ovaj dinamički sustav izgleda situacija samo s dvije različite trajektorije, što nam može pomoći da bolje razmijemo fazni portret ovog dinamičkog sustava. Fazni portret shvaćamo ga kao skup svih orijentiranih trajektorija u ravnini. Radi autonomnosti sustava, svake su dvije trajektorije ili disjuntkne, ili iste.

Ovdje imamo dvije spirale (tipa slabog fokusa) koje započinji istodobno u dvije različite točke, koje nisu na istoj trajektoriji. Radi autonomnosti sustava, ove spiralne trajektorije koje pripadaju takvim početnim točkama se se nigdje ne sijeku (tj. disjunktne su). Drugim riječima, nigdje nema preklapanja ovih dviju spirala. Trajektorije trebamo zamišljati kao da su crtane olovkom koja ostavlja trag debljine NULA.

Za razliku od eksponencijalne spirale, spirala \(r=\varphi^{-1/2}\), koja odgovara kutovima \(\varphi\in(\varphi_0,+\infty)\), ima beskonačnu duljinu.

To je dosta lako razumjeti. Pogledajmo samo dijelove te spirale u prvom kvadratnu. Na \(x_1\)-osi ti dijelovi spirala počinju u točkama koje odgovaraju vrijednostima \(\varphi_k=2\pi k\), gdje je \(k\ge k_0\). Svaki takav dio spirale ima duljinu očevidno veću od \((2\pi )^{-1/2}\). Prema tome, duljina cijele spirale ne može biti manja od zbroja $$ \sum_{k\ge k_0}(2\pi k)^{-1/2}=(2\pi )^{-1/2}\sum_{k\ge k_0}k^{-1/2}. $$ Međutim, ova zadnji red divergira (tj. zbroj mu je beskonačan), jer radi se o Dirichletovu redu s parametrom \(p=1/2\), koji je manji od jedan. Prema tome, spirala \(r=\varphi^{-1/2}\), \(\varphi>\varphi_0\), ima beskonačnu duljinu. 😊

Isti zaključak vrijedi i za bilo koju drugu spiralu oblika \(r=\varphi^{-p}\) , gdje je \(p\in(0,1]\). Ako je parametar \(p>1\), onda odgovarajuća spirala \(r=\varphi^{-p}\) ima konačnu duljinu. To je, kao što smo vidjeli, u izravnoj vezi s divergentnošću Dirichletova reda \(\sum_{k\ge k_0}k^{-p}\) za \(p>1\). Kao što znamo, za \(p=1\) dobivamo harmonijski red, koji divergira.

Ako gornji sustav zapišemo kraće kao \begin{aligned} x_1'&=- x_2-x_1\,(x_1^2+x_2^2)\\ x_2'&=\phantom{-}x_1 -x_2\,(x_1^2+x_2^2), \end{aligned} onda ga možemo shvatiti kao diferencijalnu jednadžbu \(\mathbf x'=\mathbf F(\mathbf x)\), gdje je \(\mathbf x=(x_1,x_2)^{\top}\) radius-vektor točke. U desnoj strani možemo odvojiti linearni dio (koji je blizu ishodišta dominantan) od nelinearnog kubičnog (koji je blizu ishodišta jako mali u odnosu na linearni dio): \begin{aligned} \mathbf F(\mathbf x) = \left[ \begin{matrix} -x_2\\ \phantom{-}x_1\end{matrix}\right] -(x_1^2+x_2^2) \left[ \begin{matrix} x_1\\ x_2\end{matrix}\right]= \mathbf J\mathbf x-\|\mathbf x\|^2\mathbf x. \end{aligned}

Vektor \(\mathbf J\mathbf x\) (koji je linearni dio vektorskog polja \(\mathbf F(\mathbf x)\)) djeluje tangencijalno na kružnicu na kojoj se točka nalazi, dok vektor \(-\|\mathbf x\|^2\mathbf x\) djeluje radijalno, privlačeći točku prema ishodištu. Ovaj zadnji radijalni vektor ima normu jednaku \(\|\mathbf x\|^3\), pa je po apsolutnoj vrijednosti puno manji u odnosu na njemu okomit vektor \(\mathbf J\mathbf x\) s normom \(\|\mathbf x\|\), kad je \(\mathbf x\) blizu ishodišta. Možemo zamisliti kao da se radi o kružnim trajektorijama (radi prvog vektora \(\mathbf J\mathbf x\)) koje su lagano privučene k ishodištu malim iznosom \(-\|\mathbf x\|^2\mathbf x\) (taj je kubični iznos puno manji od linearnog dijela, ako smo blizu ishodištu; na primjer unutar kruga polumjera \(1/2\) kubični dio je barem četiri puta slabiji od linearnog, a unutar kruga polumjera \(1/10\) kubični dio je barem petsto puta slabiji od linearnog). Iz tog je razloga onda jasno da će trajektorije doista biti spiralne, te da okreti postaju sve sličniji kružnicama (za razliku od eksponencijalne spirale). Pogledajte dolnje platno.

Gibanje točke duž spirale tipa slabog fokusa. Plavom bojom je označen vektor brzine \(\require{color}{\color{blue}\mathbf J\mathbf x}={\color{blue}(-x_2,x_1)^{\top}}\) koji točku vuče u pozitivnom kružnom smjeru, dok je crvenom bojom označen radijalni vektor brzine \(\require{color}{\color{red}-\|\mathbf x\|^2\mathbf x}\), koji vuče prema ishodištu. Vektor brzine gibanja točke je zbroj ta dva vektora: \(\require{color}{\color{blue}\mathbf J\mathbf x} {\color{red}-\|\mathbf x\|^2\mathbf x}\). Rezultat je spiralno gibanje (s pozitivno orijentiranim okretima), koje je sve bliže i bliže kružnom gibanju, a točka se sve sporije približava ishodištu (tj. radius kružnice se sve sporije smanjuje).

U slučaju sustava \(\mathbf x'=\mathbf J\mathbf x +\|\mathbf x\|^2\mathbf x\) imamo odbojno radijalno polje brzina, a ne privlačno. Dobivamo spiralne trajektorije (s pozitivno orijentiranim okretima), duž kojih se točka udaljuje od ishodišta, tj. spirale mijenjaju orijentaciju. Brzina udaljavanja od ishodišta sve više raste (tj. radius pripadne kružnice se sve brže povećava).

Za sustav \(\mathbf x'=-\mathbf J\mathbf x -\|\mathbf x\|^2\mathbf x\) imamo spirale s negativno orijentiranim okretima, koje se približuju ishodištu. Za sustav \(\mathbf x'=-\mathbf J\mathbf x +\|\mathbf x\|^2\mathbf x\) imamo spirale s negativno orijentiranim okretima, koje se udaljuju od ishodišta. Ishodište je stacionarna točka, koje je nestabilna.

Za nelinearni sustav \(\require{color}\mathbf x'={\color{blue}-\mathbf J\mathbf x} {\color{red}-\|\mathbf x\|^2\mathbf x}\) imamo spirale s negativno orijentiranim okretima,
koje se približuju ishodištu (kao na gornjem platnu). Ishodište je stacionarna točka, koja je stabilna.

Negativno orijentirana spirala \(r = (-\varphi)^{-1/2}\) definirana za kutove \(\varphi < \varphi_0\), gdje je \(\varphi_0 < 0\) fiksiran.
Dobiva se iz nelinearnog sustava \(\mathbf x' = -\mathbf J\mathbf x - \|\mathbf x\|^2\mathbf x\). Ishodište je stacionarna točka, koja je stabilna.

Za sustav \(\mathbf x'=-\mathbf J\mathbf x +\|\mathbf x\|^2\mathbf x\) dobivamo spirale s negativno orijentiranim okretima, koje se udaljuju od ishodišta. Ishodište je stacionarna točka, koje je nestabilna.

Više pojedinosti o dinamičkim sustavima pogledajte u [Korkut, Županović], te u predavanjima [Strogatza] o dvodimenzionalnim linearnim sustavima.


Radijalna vektorska polja

Ako je zadana bilo koja funkcija realne varijable \(f:(0,+\infty)\to\mathbb R\), onda možemo definirati odgovarajuće radijalno vektorsko polje \(\mathbf f:\mathbb R^2\to\mathbb R^2\) sa $$ \mathbf f(\mathbf x)=f(\|x\|)\frac{\mathbf x}{\|\mathbf x\|}, $$ gdje kvocijent \(\frac{\mathbf x}{\|\mathbf x\|}\) na desnoj strani predstavlja jedinični vektor smjera vektora \(\mathbf x\). Pritom vektor \(\mathbf x\in\mathbb R^2\) poistovjećujemo s točkom ravnine čiji je to radius-vektor (s početkom u ishodištu), dok sam vektor \(\mathbf f(\mathbf x)\) stavljamo s početkom u tu točku. Znači, vektorsko polje \(\mathbf f:\mathbb R^2\to\mathbb R^2\) točkama ravnine pridružujemo vektore koji polaze iz točaka ravnine.

Na primjer, za \(f(r)=ar\), gdje je \(a\) realna konstanta, dobivamo linearno (i radijalno) vektorsko polje \(\mathbf f(\mathbf x)=a\mathbf x\), koje smo već promatrali.

Za \(f(r)=r^3\) dobivamo vektorsko polje \(\mathbf f(\mathbf x)=\|x\|^3\frac{\mathbf x}{\|\mathbf x\|}=\|\mathbf x\|^2\mathbf x\). Pogledajmo vizualizaciju tog polja na sljedećem platnu.

Radijalno vektorsko polje \(\mathbf f\) koje svakoj točki s radius-vektorom \(\mathbf x\) pridružuje vektor \(\mathbf f(\mathbf x)=-\|\mathbf x\|^2x\), orijentiran (usmjeren) prema ishodištu. Prikazani su vektori polja samo na točkama koncentričnih kružnica oko ishodišta. Izvan kruga polumjera \(1\) je duljina vektora \(\mathbf f(\mathbf x)\) veća od radiusa odgovarajuće kružnice, a izvan kruga polumjera \(\sqrt2\) mu je duljina veća od promjera (tj. \(r^3>2r\)).

Radijalni dinamički sustav oblika \(\mathbf x'=-\|\mathbf x\|^2\mathbf x\) ima trajektorije koje radijalni intervali od odabrane početne točke (koju biramo mišem, pritisnutim stalno u toj točki). Ako točku odaberemo dovoljno daleko od ishodišta, onda ona krene razmjerno velikom brzinom prema ishodištu. Odabrana točka nikada ne stiže do ishodišta, ali mu se stalno približava. Ako početnu točku odaberemo bliže ishodišta, početna brzina je vrlo mala. Fazni portret ovog sustava sastoji se od radijalnih zraka, orijentiranih prema ishodištu. Samo ishodište je također jedna trajektorija, u kojoj točka stoji na miru (stacionarna je, tj. mirna točka). Ishodište je stabilna točka, jer sve trajektorije konvergiraju prema njoj, kada \(t\to+\infty\), iako vrlo sporo (točnu \(\varepsilon-\delta\) definiciju stabilne stacionarne točke pogledajte u [Korkut, Županović], ili u [Strogatz]). Štoviše, ishodište je atraktor (privlačna točka), jer sve točke k njoj konvergiraju kada \(t\to+\infty\)

Radijalni dinamički sustav oblika \(\mathbf x'=\|\mathbf x\|^2\mathbf x\), gdje je \(\mathbf x=\mathbf x(t)\) (primijetite da smo samo promijenili predznak desne strane u odnosu na predhodni primjer), u komponentnom zapisu glasi \begin{aligned} x_1'&=x_1(x_1^2+x_2^2)\\ x_2'&=x_2(x_1^2+x_2^2). \end{aligned} Sustav je odbojan s obzirom na ishodište.

Radijalni dinamički sustav oblika \(\mathbf x'=\|\mathbf x\|^2\mathbf x\), gdje je \(\mathbf x=\mathbf x(t)\), ima trajektorije koje su radijalne zrake od odabrane početne točke (koju biramo mišem, pritisnutim stalno u toj točki). Ako točku odaberemo dovoljno daleko od ishodišta, onda ona krene razmjerno velikom brzinom u smjeru suprotnom od ishodišta. Ako početnu točku odaberemo bliže ishodištu, početna brzina je vrlo mala. Fazni portret ovog sustava sastoji se od radijalnih zraka, orijentiranih suprotno od ishodišta. Samo ishodište je također jedna trajektorija, u kojoj točka stoji na miru (stacionarna je, tj. mirna točka). Ishodište je nestabilna točka, jer sve se trajektorije udaljuju od nje kada \(t\to+\infty\), i to sve većom brzinom. Štoviše, ishodište je odbojna točka (engl. repeller), jer se sve točke od nje udaljuju kada \(t\to+\infty\).

Pogledajmo još kako za predhodni primjer izgleda odgovarajuće vektorsko polje, koje je radijalno.

Odbojno radijalno vektorsko polje \(\mathbf f\) koje svakoj točki s radius-vektorom \(\mathbf x\) pridružuje vektor (brzine) \(\mathbf f(\mathbf x)=\|\mathbf x\|^2\mathbf x\) orijentiran suprotno od ishodišta. Prikazani su vektori polja samo na točkama koncentričnih kružnica oko ishodišta. Izvan kruga polumjera \(1\) je duljina vektora \(\mathbf f(\mathbf x)\) veća od polumjera odgovarajuće kružnice.

Radijalna vektorska polja sa singularitetom u ishodištu

U ovom odjeljku radi praktičnosti rabimo pojam singulariteta vektorskog polja u drugačijem smislu nego u [Korkut, Županović] (gdje singularna točka znači stacionarnu točku, tj. ravnotežnu točku dinamičkog sustava). Za radijalno vektorsko polje \(\mathbf x\mapsto \mathbf{Fx}\) kažemo da u ishodištu ima singularitet, ako \(\|\mathbf F(\mathbf x)\|\to+\infty\) kada \(\|\mathbf x\|\to0\). (U samom ishodištu vektorsko polje nije definirano.) To će biti slučaj ako je recimo \(\|\mathbf F(\mathbf x)\|=K\|\mathbf x\|^{-2}\), kao u sljedećem primjeru.

Pogledajmo radijalno vektorsko polje \(\mathbf F\) koje svakoj točki s radius-vektorom \(\mathbf x\) pridružuje vektor brzine $$\mathbf F(\mathbf x)=\frac {K}{\|\mathbf x\|^{2}}\frac{\mathbf x}{\|\mathbf x\|},$$ gdje je \(K>0\) konstanta (na platnu je uzeto \(K=1\)). Vektorsko polje je orijentirano suprotno od ishodišta. Vektor \(\frac{\mathbf x}{\|\mathbf x\|}\) je kao i obično jedinični vektor smjera polja. Prikazani su vektori polja samo u točkama koncentričnih kružnica oko ishodišta (koje ćete vidjeti povlačenjem miša po platnu). Jačina polja opada s kvadratom udaljenosti od ishodišta.

Dobivamo dinamički sustav oblika \(\mathbf x'=\frac{K}{\|\mathbf x\|^2}\frac{\mathbf x}{\|\mathbf x\|}\), gdje je \(\mathbf x=\mathbf x(t)\) i \(K>0\).

Zapisan u komponentama, taj sustav glasi \begin{aligned} x_1'&=\frac{K}{x_1^2+x_2^2}\frac{x_1}{\sqrt{x_1^2+x_2^2}}\\ x_2'&=\frac{K}{x_1^2+x_2^2}\frac{x_2}{\sqrt{x_1^2+x_2^2}}. \end{aligned} Upravo ovakve desne strane smo koristili za prikaz vektorskog polja na gornjem platnu.

Početnu vrijednost \(\mathbf x(0)=\mathbf x_0\) biramo tako da bude \(\ne 0\) (tj. izvan ishodišta), jer u ishodištu vektorsko polje nije definirano.

Dinamički sustav oblika \(\mathbf x'=\frac{K}{\|\mathbf x\|^2}\frac{\mathbf x}{\|\mathbf x\|}\), gdje je \(\mathbf x=\mathbf x(t)\) i \(K>0\), ima trajektorije koje su radijalne zrake od odabrane početne točke (koju biramo mišem, pritisnutim stalno u toj točki). Ako točku odaberemo dalje od ishodišta, onda ona krene razmjerno malom brzinom u smjeru suprotnom od ishodišta. Ako početnu točku odaberemo bliže ishodištu, početna brzina je vrlo velika. Fazni portret ovog sustava sastoji se od radijalnih zraka, orijentiranih suprotno od ishodišta.

Jednostavnim integralnim računom pokazuje se da je \(\|\mathbf x(t)\|=(3Kt+\|\mathbf x_0\|^3)^{1/3}\), gdje je \(t\ge0\). Posebno, \(\|\mathbf x(t)\| \asymp t^{1/3}\) kada \(t\to+\infty\) (tj. omjer lijeve i desne strane uz \(\asymp\) je između dviju pozitivnih konstanata neovisnih o \(t>0\)).

Doista, ako zraku koja spaja ishodište s točkom \(\mathbf x_0\) označimo kao \(r\)-os, onda je \(r'=Kr^{-2}\), tj. \(r^2dr=K\,dt\). Integriranjem dobivamo \(\frac13r^3=Kt+C\), a iz početnog uvjeta slijedi da je \(C=\frac 13r_0^3\), gdje je \(r_0=\|\mathbf x_0\|\) početni položaj točke na \(r\)-osi. Prema tome je \(r(t)=(3Kt+r_0^3)^{1/3}\). Upravo ova formula nam je poslužila za crtanje trajektorija na gornjem platnu.

Pogledajmo privlačno radijalno vektorsko polje brzina \(\mathbf F\) koje svakoj točki s radius-vektorom \(\mathbf x\) pridružuje vektor $$\mathbf F(\mathbf x)=\frac {K}{\|\mathbf x\|^{2}}\frac{\mathbf x}{\|\mathbf x\|}$$ orijentiran prema ishodištu. Ovdje je \(K<0\) (na platnu uzimamo \(K=-1\)) Vektor \(\frac{\mathbf x}{\|\mathbf x\|}\) je kao i obično jedinični vektor smjera polja. Prikazani su vektori polja samo na točkama koncentričnih kružnica oko ishodišta (koje ćete vidjeti povlačenjem miša po platnu). Jačina polja opada s kvadratom udaljenosti od ishodišta.

Dinamički sustav oblika \(\mathbf x'=\frac{K}{\|\mathbf x\|^2}\frac{\mathbf x}{\|\mathbf x\|}\), gdje je \(\mathbf x=\mathbf x(t)\) i \(K<0\), ima trajektorije koje su radijalne zrake od odabrane početne točke (koju biramo mišem, pritisnutim stalno u toj točki). Ako točku odaberemo dalje od ishodišta, onda ona krene razmjerno malom brzinom u smjeru prema ishodištu. Ako početnu točku odaberemo bliže ishodištu, početna brzina je vrlo velika.

Fazni portret ovog sustava sastoji se od radijalnih zraka, orijentiranih prema ishodištu. Jednostavnim integralnim računom pokazuje se da je \(\|\mathbf x(t)\|=(3Kt+\|\mathbf x_0\|^3)^{1/3}\), gdje je \(0\le t\le -\frac1{3K}\|\mathbf x_0\|^3\) (podsjećamo da je konstanta \(K\) negativna). Svaka točka \(\mathbf x_0\ne0\) kroz konačno vrijeme \(t=-\frac1{3K}\|\mathbf x_0\|^3\) "udari" beskonačnom brzinom u ishodište. U ishodištu vektorsko polje nije definirano, pa se ne može govoriti o stabilnosti ishodišta.

U svim primjerima u ovom i predhodnom odjeljku riječ je o radijalnim dinamičkim sustavima oblika \(\mathbf x'=g(\|\mathbf x\|)\,\mathbf x\), pri čemu je funkcija \(g:(0,\infty)\to\mathbb R\) uvijek istog predznaka: bilo pozitivnog bilo negativnog. U ta dva slučaja imamo ili odbojno ili privlačno radijalno polje. Jasno je da su trajektorije iste kao i u najobičnijim linearnim sustavima \(\mathbf x'=\mathbf x\) i \(\mathbf x'=-\mathbf x\) (gdje je \(\mathbf A=\pm\mathbf I\)), kakve smo promatrali na početku ovog priloga (\(\mathbf x'=\mathbf A\mathbf x\), za matrice \(\mathbf A\) oblika \(a\mathbf I\)). Trajektorije su iste, ali radijalna brzina nije ista (međutim je istog predznaka i za nelinearni i za njemu pridružen linearni sustav, u kojem smo samo ispustili \(g(\|\mathbf x\|)\), osim njegova predznaka).

Vektorsko polje indeksa \(n\)

Već smo vidjeli primjer vektorskog polja indeksa \(1\) (cirkularno vektorsko polje, radijalno vektorsko polje), kao i primjer vektorskog polja indeksa \(-1\) (hiperboličko vektorsko polje).

Kako bismo konstruirali vektorsko polje bilo kojeg zadanog indeksa \(n\in\mathbb Z\)? U tome nam mogu pomoći funkcije kompleksne varijable. Ako označimo sa \(z=x_1+x_2i\in\mathbb C\) kompleksni broj koji odgovara točki \((x_1,x_2)\) u ravnini, onda će funkcija kompleksne varijable $$f(z)=z^n$$ generirati vektorsko polje sa željenim svojstvom. Doista, ako u Gaussovoj ravnini gledamo kompleksni broj \(e^{i\varphi}\) na jediničnoj kružnici (koji obilazi kružnicu jednom u pozitivnom smjeru, kada \(\varphi\in[0,2\pi\)), onda je radi Eulerove formule $$ f(e^{i\varphi})=(e^{i\varphi})^n=e^{in\varphi}, $$ pa dobivamo \(n\) odgovarajuíh okreta u Gaussovoj ravnini oko ishodišta (i to u pozitivnom smjeru ako je \(n\) pozitivan cijeli broj, a u negativnom ako je cijeli broj \(n\) negativan). Drugim riječima, jednom okretu kompleksnog broja \(z\) oko ishodišta u pozitivnom smjeru, odgovara \(n\) okreta kompleksnog broja \(f(z)=z^n\) oko ishodišta (u smjeru određenom predznakom broja \(n\)).

Prema tome, ako definiramo \(u(x_1,x_2)\) kao realni dio od \(z^n\), a \(v(x,y)\) kao imaginarni dio od \(z^n\), onda će vektorsko polje \((x_1,x_2)\mapsto(u(x_1,x_2), v(x_1,x_2))\) imati analogno svojstvo, tj. bit će indeksa \(n\) u odnosu na ishodište.

Na primjer, budući da za \(n=2\) vrijedi \((x_1+ix_2)^2=(x_1^2-x_2^2)+2x_1x_2i\), dobivamo kao odgovarajuće vektorsko polje \((x_1, x_2)\mapsto(x_1^2-x_2^2, 2x_1x_2)\), koje je indeksa \(2\). To nam zorno pokazuje sljedeće platno, kojim smo vizualizirali to vektorsko polje.

Ako je cijeli broj \(n\) negativan, onda uporabom konjugirano-kompleksnog broja \(\overline{z}\) možemo pisati $$f(z)=z^n=\frac1{z^{|n|}}\frac{\overline{z^{|n|}}}{\overline{z^{|n|}}}=\frac{\overline{z}^{|n|}}{|z|^{2|n|}}$$ Budući da je \(|z|^{2|n|}>0\) za sve \(z\ne 0\), zaključujemo da za \(n<0\) vektorska polja generirana (odvajanjem realnog i imaginarnog dijela) sa \(z^n\) i \(\overline {z^{|n|}}\) imaju iste indekse u odnosu na ishodište.


Indeks vektorskog polja \((x_1,x_2)\mapsto(x_1^2-x_2^2,2x_1x_2)\) u odnosu na ishodište jednak je \(2\): ako pritisnutim mišem napravimo jedan okret oko ishodišta u pozitivnom smjeru (tj. u smjeru suprotnom od smjera kazaljke na satu), strjelica napravi dva okreta u pozitivnom smjeru. Općenitu definiciju indeksa vidi u [Korkut, Županović].

Umjesto da za \(n=-2\) računamo realni i imaginarni dio od \(1/z^2\), dovoljno je u predhodnom primjeru gledati "konjugirano kompleksno" polje, u kojem samo promijenimo predznak druge komponente: $$(x_1,x_2)\mapsto(x_1^2-x_2^2,-2x_1x_2).$$ Ovo je vektorsko polje indeksa \(-2\) u odnosu na ishodište, što nam zorno pokazuje sljedeće platno.


Indeks vektorskog polja \((x_1,x_2)\mapsto(x_1^2-x_2^2,-2x_1x_2)\) u odnosu na ishodište jednak je \(-2\): ako pritisnutim mišem napravimo jedan okret oko ishodišta u pozitivnom smjeru (tj. u smjeru suprotnom od smjera kazaljke na satu), strjelica napravi dva okreta u negativnom smjeru.

Možemo se lako uvjeriti da se za \(n=-1\), tj. preko \(f(z)=z^{-1}\) dobiva hiperboličko vektorsko polje. Budući da je \(\frac 1z=\frac{x_1-ix_2}{x_1^1+x_2^2}\), dovoljno je gledati vektorsko polje \(u(x_1,x_2)=x_1\) i \(u(x_1,x_2)=-x_2\). To je doista hiperboličko polje, koje smo već promatrali ranije.

Pogledajmo polinomijalno polje indeksa \(3\), generirano sa \(f(z)=z^3=(x_1+ix_2)^3\). U ovom vektorskom polju \((x_1,x_2)\mapsto(u(x_1,x_2),v(x_1,x_2))\) je \(u=\mbox{Re}(z^3)=x_1^3-3x_1x_2^2\) i \(v=\mbox{Im}(z^3)=3x_1^2x_2-x_3^3\). Uvjerite se na sljedećem platnu da je indeks tog polja odnosu na ishodište jednak \(3\).


Indeks vektorskog polja \((x_1,x_2)\mapsto(x_1^3-3x_1x_2^2,3x_1^2x_2-x_3^3)\) u odnosu na ishodište jednak je \(3\): ako pritisnutim mišem napravimo jedan okret oko ishodišta u pozitivnom smjeru (tj. u smjeru suprotnom od smjera kazaljke na satu), strjelica napravi tri okreta u pozitivnom smjeru.
Zanimljivo je da ako mišem napravimo okret točke od trećine punog kuta (tj. \(2\pi/3\)) radijana oko ishodišta (tj. \(\frac{\pi}2+\frac{\pi}6\)), onda strjelica vektorskog polja napravi jedan puni okret. To je naravno posljedica Eulerove formule.

Pogledajmo još vektorsko polje indeksa \(-3\) u odnosu na ishodište. Dobijemo ga tako da jednostavno promijenimo predznak druge komponente vektorskog polja u predhodnom primjeru (tj. konjugiramo kompleksni broj \(z^3\)).


Indeks vektorskog polja \((x_1,x_2)\mapsto(x_1^3-3x_1x_2^2,-3x_1^2x_2+x_3^3)\) u odnosu na ishodište jednak je \(-3\): ako pritisnutim mišem napravimo jedan okret oko ishodišta u pozitivnom smjeru (tj. u smjeru suprotnom od smjera kazaljke na satu), strjelica napravi tri okreta u negativnom smjeru.

Kako izgledaju trajektorije dinamičkog sustava opisanog sa \begin{aligned} x_1'&=u(x_1,x_2)\\ x_2'&=v(x_1,x_2), \end{aligned} u četiri predhodna slučaja, gdje su \(x_1=x_1(t)\), \(x_2=x_2(t)\) nepoznate funkcije? Odgovor na to pitanje daje nam sljedeća fotografija, objavljena u članku [Scheuermann, Hagen, Krüger, Menzel, Rockwood]:


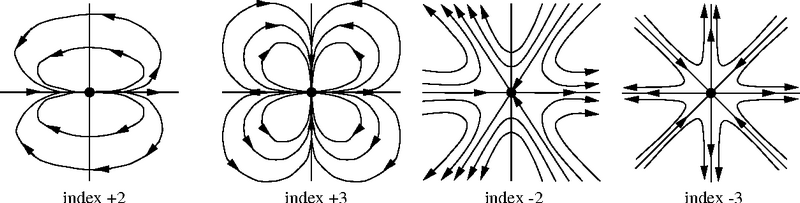
Možete sami za vježbu nazrijeti ove trajektorije, slijedeći tok vektorskog polja na gornja četiri platna. Naravno, iste takve trajektorije imaju i rješenja jednadžbe \(z'=z^n\) u Gaussovoj ravnini, za \(n=2,\,3,\,-2,\,-3\), gdje je \(z=z(t)\).

Pojam indeksa postaje još jasniji ako na platnu crtamo radius vektor točke, a odgovarajuće vektorsko polje crtamo ne iz te (pomične) točke, nego iz ishodišta. Taj vektor ostavljamo u crvenoj boji. Time vektorsko polje više nije prikazano na uobičajen način, kada početak vektora stavljamo u točku u kojoj se on izračunava. Radi toga govorimo o vektorskom preslikavanju, umjesto o vektorskom polju.


Indeks vektorskog preslikavanja \((x_1,x_2)\mapsto(x_1^2-x_2^2,2x_1x_2)\) u odnosu na ishodište jednak je \(2\): ako pritisnutim mišem napravimo jedan okret oko ishodišta u pozitivnom smjeru (tj. u smjeru suprotnom od smjera kazaljke na satu), crvena strjelica (vektorskog polja, translatiranog u ishodište) napravi dva okreta u pozitivnom smjeru.
Ako platno gledamo kao Gaussovu (kompleksnu) ravninu, onda se kompleksni broj \(z\) preslikava u \(z^2\).


Indeks vektorskog preslikavanja \((x_1,x_2)\mapsto(x_1^2-x_2^2,-2x_1x_2)\) u odnosu na ishodište jednak je \(-2\): ako pritisnutim mišem napravimo jedan okret oko ishodišta u pozitivnom smjeru (tj. u smjeru suprotnom od smjera kazaljke na satu), strjelica napravi dva okreta u negativnom smjeru.
Ovime smo vizualizirali pridruživanje \(z\mapsto \overline{z^2}\), pri čemu su vektori (kompleksni brojevi) \(\overline{z^2}\) ne samo paralelni, nego i iste orijentacije kao i \(1/{z^2}\). Prema tome, pridruživanje \(z\mapsto 1/{z^2}\) u Gaussovoj ravnini ima također indeks \(-2\) u odnosu na ishodište.


Indeks vektorskog preslikavanja \((x_1,x_2)\mapsto(x_1^3-3x_1x_2^2,3x_1^2x_2-x_3^3)\) u odnosu na ishodište jednak je \(3\): ako pritisnutim mišem napravimo jedan okret oko ishodišta u pozitivnom smjeru (tj. u smjeru suprotnom od smjera kazaljke na satu), strjelica napravi tri okreta u pozitivnom smjeru.
Gledajući u Gaussovoj ravnini, ovo predstavlja vizualizaciju pridruživanja \(z\mapsto z^3\), koje je indeksa \(3\) u odnosu na ishodište.

Pogledajmo još vektorsko preslikavanje indeksa \(-3\) u odnosu na ishodište. Dobijemo ga tako da jednostavno promijenimo predznak druge komponente vektorskog polja u predhodnom primjeru.


Indeks vektorskog preslikavanja \((x_1,x_2)\mapsto(x_1^3-3x_1x_2^2,-3x_1^2x_2+x_3^3)\) u odnosu na ishodište jednak je \(-3\): ako pritisnutim mišem napravimo jedan okret oko ishodišta u pozitivnom smjeru (tj. u smjeru suprotnom od smjera kazaljke na satu), strjelica napravi tri okreta u negativnom smjeru.
Gledajući u Gaussovoj ravnini, ovo predstavlja vizualizaciju pridruživanja \(z\mapsto \overline{z^3}\), koje je indeksa \(-3\) u odnosu na ishodište. Vektori \(\overline{z^3}\) su ne samo paralelni, nego i iste orijentacije, pa i pridruživanje \(z\mapsto 1/z^3\) ima indeks jednak \(-3\) u odnosu na ishodište.

Trajektorije vektorskog polja indeksa dva u ishodištu. On odgovara dinamičkom sustavu \(z'=z^2\) zadanom u Gaussovoj ravnini, tj. (po komponentama) dinamičkom sustavu \(x_1'= x_1^2-x_2^2\), \(x_2'=2x_1x_2)\). Budući da je apsolutna vrijednost brzine točke na položaju kompleksnog broja \(z\) jednaka \(|z'|=|z^2|=|z|^2\), zaključujemo da je brzina blizu ishodišta vrlo mala, a za udaljene točke velika (brzina raste s kvadratom udaljenosti točke od ishodišta). Može se pokazati da su trajektorije ili kružnice bez ishodišta, ili pak samo ishodište. Usporedite dobivene trajektorije s onima na prvoj od četriju sličica iz članka [Scheuermann, Hagen, Krüger, Menzel, Rockwood], prikazanoj gore.

U predhodnom primjeru, ishodište je polustabilna točka (s lijeve strane od ishodišta vektorsko polje brzina je privlačno prema ishodištu, dok je s desne strane odbojno od ishodišta):

  • na vodoravnoj osi, ishodište je stabilna točka s obzirom na lijevu poluos (tj. ako je \(z_0\) početna točka lijevo od ishodiše, onda se ona s vremenom približava prema ishodištu),
  • na vodoravnoj osi, ishodište je nestabilna točka s obzirom na desnu poluos (tj. ako je \(z_0\) početna točka desno od ishodišta, onda se ona s vremenom udaljuje od ishodišta duž te osi).

Opišimo vrlo kratko kako je dobivena dinamika vidljiva na gornjem platnu. Pišući diferencijalnu jednadžbu \(z'=z^2\) (u skupu kompleksnih brojeva!) kao \(z^{-2}dz=dt\), integriranjem dobivamo \(-z^{-1}=t+C\), gdje je \(C\) neka konstanta (kompleksni broj!). Za zadani početni uvjet \(z(0)=z_0\ne0\) dobivamo kao rješenje \(z(t)=(z_0^{-1}-t)^{-1}\). Odgovarajuća realna rješenja \(x_1(t)\) i \(x_2(t)\) dobivamo kao realni i imaginarni dio od \(z(t)\), jer je \(z(t)=x_1(t)+i\,x_2(t)\). Početna vrijednost \(z_0\) zadaje se strjelicom miša na platnu (kada pritisnemo tipku miša), a položaji \(z(t)\) izračunavaju se 'pod platnom' (tj. u Vašem računalu) od trenutka \(t=0\) do momenta odpuštanja tipke miša.

Kao što vidimo na temelju opisa dinamike, trajektorije rješenja jednadžbe \(z'=z^2\) na gornjem platnu nalikuju na trajektorije oko dipola (na primjer električkog dipola učvršćenog u ishodištu, tipa \(-+\), vodoravno usmjerenog, koje djeluje na slobodnu česticu pozitivnog naboja, čiji početni položaj na platnu zadajemo strjelicom miša). Iako trajektorije izgledaju "realistično", brzine očevidno nisu realistične. Naime, blizu ishodišta bi vektor brzine velikog iznosa, a na većoj udaljenosti sve manji (a ne obratno).

U predhodnom primjeru je brzina točke po aspolutnoj vrijednosti jednaka \(|z'|=|z|^2\), tj. jednaka je kvadratu udaljenosti točke od ishodišta. Reparametrizacijom vremena možemo postići da brzina točke \(|z'|\) ovisi kao \(1/|z|\) od trenutnog položaja \(z\) (kada \(|z|\to0\) ili kada \(|z|\to\infty\)): ako je točka blizu ishodišta, brzina je velika (radi jakog djelovanja dipola), a ako je točka daleko, brzina je mala (radi slabog djelovanja dipola). Dobivamo iste trajektorije kao u predhodnom primjeru, ali razdioba brzina duž trajektorije (putanje) točke pod djelovanjem dipola (vodoravno položenog u ishodištu) je realističnija.


Literatura

  • Neven Elezović: Kompleksni brojevi, Element, Zagreb
  • Neven Elezović, Andrea Aglić Aljinović, Darko Žubrinić: Linearna algebra, Element, Zagreb 2020.
  • Luka Korkut i Vesna Županović: Diferencijalne jednadžbe i teorija stabilnosti, Element, Zagreb 2009.
  • Steven Strogatz (istaknuti stručnjak za dinamičke sustave): Two dimensional linear systems, video snimak predavanja, traje 1 sat i 15 min.
  • Steven Strogatz: Nonlinear dynamics and chaos [PDF] (za ambicioznije);
    video snimci predavanja:
  • Gerik Scheuermann, Hans Hagen, Heinz Krüger, Martin Menzel, Alyn P. Rockwood: Visualization of higher order singularities in vector fields, 1997 Computer Science Proceedings. Visualization '97



Matematika za osnovne i srednje škole

Matematičke šale

History of Croatian science

Školovanje Nikole Tesle u Hrvatskoj